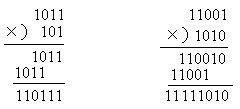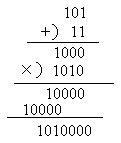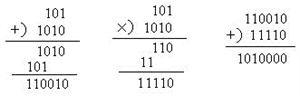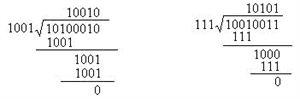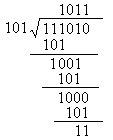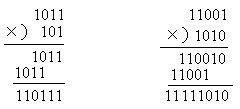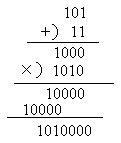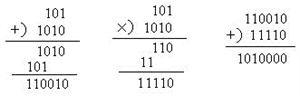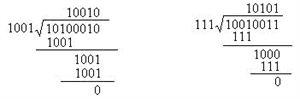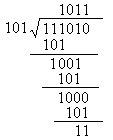二进制的四则运算的方法介绍

二进制四则运算和十进制四则运算原理相同，所不同的是十进制有十个数码，“满十进一”，二进制只有两个数码0和1，“满二进一”。二进制运算口诀则更为简单。 1．加法 二进制加法，在同一数位上只有四种情况： 0＋0＝0，0＋1＝1，1＋0＝1，1＋1＝10。 只要按从低位到高位依次运算，“满二进一”，就能很容易地完成加法运算。 例1 二进制加法 （1）10110＋1101； （2）1110＋101011。 解 加法算式和十进制加法一样，把右边第一位对齐，依次相应数位对齐，每个数位满二向上一位进一。 10110＋1101＝100011 1110＋101011＝111001 通过计算不难验证，二进制加法也满足“交换律”，如101＋1101＝1101＋101＝10010。 多个数相加，先把前两个数相加，再把所得结果依次与下 一个加数相加。 例2 二进制加法 （1）101＋1101＋1110； （2）101＋（1101＋1110）。 解 （1）101＋1101＋1110 （2）101＋（1101＋1110） ＝10010＋1110 ＝101＋11011 ＝100000； ＝100000 从例2的计算结果可以看出二进制加法也满足“结合律”。 巩固练习 二进制加法 （1）1001＋11； （2）1001＋101101； （3）（1101＋110）＋110； （4）（10101＋110）＋1101。 2．减法 二进制减法也和十进制减法类似，先把数位对齐，同一数位不够减时，从高一位借位，“借一当二”。 例3 二进制减法 （1）11010－11110； （2）10001－1011。 解（1）110101－11110＝10111； （2）10001－1011＝110。 例4 二进制加减混合运算 （1）110101＋1101－11111； （2）101101－11011＋11011。 解（1）110101＋1101－11111 ＝1000010－11111 ＝100011 （2）101101－11011＋11011 ＝10011＋11011 ＝101101。 巩固练习 二进制运算 （1）11010－1101； （2）11001－111； （3）110101－1111＋101； （4）1001＋1110－10011。 3．乘法 二进制只有两个数码0和1，乘法口诀只有以下几条： 0×0＝0，0×1＝0，1×0＝0，1×1＝1 概括成口诀：零零得零，一零得零，一一得一。 二进制乘法算式和十进制写法也一样。 例5 二进制乘法 （1）1001×101； （2）11001×1010。 解 （1）1011×101＝110111；（2）11001×1010＝11111010。 例6 二进制运算 （1）101×1101； （2）1101×101； （3）（101＋11）×1010； （4）101×1010＋11×1010。 解（1） （2） 101×1101＝1000001； 1101×101＝1000001； （3） （101＋11）×1010＝1010000； （4） 101×1010＋11×1010＝1010000 从例6的计算结果可以看出，二进制乘法满足“交换律”；乘法对加法也满足“分配律”。对这一结论，大家还可以进行多次验证。 巩固练习 二进制运算 （1）1011×1101； （2）11101×1001； （3）10101×（111＋101）； （4）（11001－1111）×101 4．除法 除法是乘法的逆运算，二进制除法和十进制除法也一样，而且更简单，每一位商数不是0，就是1。 例7 二进制除法 （1）10100010÷1001； （2）10010011÷111。 解 （1） （2） 10100010÷1001＝10010； 10010011÷111＝10101。 例8 求二进制除法的商数和余数 111010÷101 解 111010÷101 所得商数是1011，余数是11。 巩固练习 二进制除法 （1）1101110÷101； （2）1010110001÷1101； （3）求商数和余数 1101001÷1001 在二进制除法中，被除数，除数，商数和余数的关系和十进制除法的关系是相同的。 被除数＝除数×商数＋余数。 如例8，111010＝101×1011＋11。

本文地址：http://www.45fan.com/a/question/42778.html