容斥的原理有哪些？

在一些计数问题中，经常遇到有关集合元素个数的计算。我们用|A|表示有限集A的元素个数。在并集的讨论中，已经知道，求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成 |A∪B|=|A|+|B|-|A∩B| 我们称这一公式为包含与排除原理，简称容斥原理。 包含与排除原理告诉我们，要计算两个集合A、B的并集A∪B的元素的个数，可分以下两步进行： 第一步 分别计算集合A、B的元素个数，然后加起来，即先求|A|+|B|（意思是把A、B的一切元素都“包含”进来，加在一起）； 第二步 从上面的和中减去交集的元素个数，即减去|A∩B|（意思是“排除”了重复计算的元素个数）。 例1 求不超过20的正整数中是2的数倍或3的倍数的数共有多少个。 分析与解：设I=｛1，2，3，…，19，20｝，A=｛I中2的倍数｝，B=｛I中3的倍数｝。 显然，题目要求计算并集|A∪B|的元素个数，即求|A∪B|。 易知， A=｛2，4，6，…，18，20｝， 共有10个元素，即|A|=10， B=｛3，6，9，12，15，18｝， 共有6个元素，即|B|=6。 A∩B=｛I中既是2的倍数又是3的倍数｝ =｛6，12，18｝ 共有3个元素，即|A∩B|=3，所以 |A∪B|=|A|+|B|-|A∩B| =10+6-3=13 答：所求的数共有13个。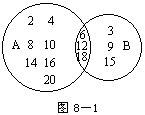 此题可直观地图示如下： 图8-1中，A表示不超过20的正整数中2的倍数的集合。B表示不超过20的正整数中3的倍数的集合。在不超过20的正整数中既是2的倍数又是3的倍数的数有6，12，18，即A∩B中的数。 例2 某班统计考试成绩，数学得90分上的有25人；语文得90分以上的有21人；两科中至少有一科在90以上有38人。问两科都在90分以上的有多少人？（1985年初一迎春杯数学竞赛试题） 解：设A=｛数学成绩90分以上的学生）， B=｛语文成绩90分以上的学生｝。 那么，集合A∪B表示两科中至少有一科在90分以上的学生，由题意知 |A|=25，|B|=21，A∪B=38。 现在要求两科都在90分以上的学生人数，即求|A∩B|。由容斥原理得 |A∩B|=|A|+|B|-|A∪B|=25+21-38=8 答：两科都在90分以上的学生有8人。 在计算面积的问题中，有时也要用到容斥原理。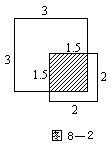 例3 边长为2的正方形与边长为3的正方形，如图8—2放在桌面上，它们所盖住的面积有多大？ 分析与解：如果把两个正方形的面积加起来，得 22+32=13 就会发现，多计算了一块阴影部分面积。这块面积是1.52=2.25。应该从上面的和中减去这一部分。因此，两个正方形所盖住的面积应是 22+32-1.52 =13-2.25=10.75 答：两个正方形所盖住的面积是10.75。 例4 有100位旅客，其中有10人既不懂英语又不懂俄语，有75人懂英语，83人懂俄语。问既懂英语又懂俄语的有多少人？（1985年小学迎春杯数学竞赛试题） 分析与解：设A=｛懂英语的旅客｝，B=｛懂俄语的旅客｝。那么，英语和俄语这两种语言中至少懂一种的旅客的集合为A∪B，而两种语言都懂的旅客的集合为A∩B。题目要求|A∩B|。 由题意知，|A|=75，|B|=83，|A∪B|=100-10=90。由容斥原理，得 |A∩B|=|A|+|B|-|A∪B| =75+83-90=68 答：既懂英语又懂俄语的旅客有68人。 对于任意三个有限集合A、B、C，我们可以将上面的容斥原理推广得到如下的公式： |A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|。 三个集合的容斥原理告诉我们，要计算并集A∪B∪C的元素个数，可以分三步进行： 第一步 求|A|+|B|+|C|； 第二步 减去|A∩B|，|A∩C|，|B∩C|； 第三步 加上|A∩B∩C|。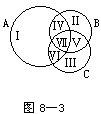 结合图8—3还可以作出如下说明。由于A∪B∪C一般可分成如图的七个部分，或者说分成了七个不相交的子集。其中Ⅰ、Ⅱ、Ⅲ部分的元素仅属于某个集合，而Ⅳ、V、Ⅵ部分的元素分别属于某两个集合，第Ⅶ部分则是三个集合的交集由于A∪B∪C的元素分别来自集合A、B、C，因此，先计算|A|+|B|+|C|。在这个和里，Ⅰ、Ⅱ、Ⅲ部分的元素只计算了一次，而Ⅳ、V、Ⅵ部分的元素各计算了两次，第Ⅶ部分（A∩B∩C）的元素计算了三次。在第二步减去|A∩B|，|A∩C|，|B∩C|后得 |A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|。 这样显然消除了IV、V、VI部分的重复计算，但同时连续三次减去了第Ⅶ部分，于是第Ⅶ部分的元素个数都被减去了，因此必须补上第Ⅶ部分的元素个数，即再加上|A∩B∩C|，综上所述得 |A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|。 例5 某校组织棋类比赛，分成围棋、中国象棋和国际象棋三个组进行。参加围棋比赛的共有42人，参加中国象棋比赛的共有51人，参加国际象棋比赛的共有30人。同时参加了围棋和中国象棋比赛的共有13人，同时参加了围棋和国际象棋比赛的7人，同时参加了中国象棋和国际象棋比赛的11人，其中三种棋赛都参加的3人。问参加棋类比赛的共有多少人？ 解法1：设A=｛参加围棋比赛的人｝，B=｛参加中国象棋比赛的人｝，C=｛参加国际象棋比赛的人｝，那么参加棋类比赛的人的集合为A∪B∪C。由题意知： |A|=42，|B|=，|C|=30， |A∩B|=13，|A∩C|=7，|B∩C|=11， |A∩B∩C|=3。 由容斥原理得 |A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∪C|-|B∩C|+|A∩B∩C| =42+51+30-13-7-11+3 =95（人） 答：参加棋类比赛的共有95人。 解法2：利用文氏图逐个填写各区域所表示的集合元素的个数，然后求出最后结果。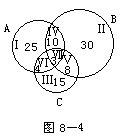 设A、B、C分别表示参加围棋、中国象棋和国际象棋比赛的人的集合。其文氏图分割成七个互不相交的区域。区域Ⅶ（即A∩B∩C）表示三种棋赛都参加的数的集合。由题意应填数字3。区域IV表示仅参加围棋和中国象棋两项比赛的人的集合，其人数为13-3=10（人）。区域Ⅵ表示仅参加围棋和国际象棋两项比赛的人的集合，其人数为7-3=4（人）。区域Ⅰ表示只参加围棋一项比赛的人的集合，其人数为42-10-4-3=25（人）。同理可把区域Ⅱ、Ⅲ、V所表示的集合的人数逐个算出，分别填入相应的区域内（图8—4）。由此得出参加棋类比赛的总人数为 25+30+15+15+10+8+4=3=95 说明：解法2简单直观，不易出错。由于各个区域所表示的集合的元素个数都计算出来了，因此提供了较多的信息，易于回答各种方式的提问。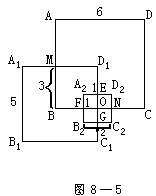 例6 边长分别为6，5，2的三个正方形，如图8—5所示放在桌面上。问它们盖住的面积是多大？ 分析与解：这个问题可用容斥原理来解。设R表示正方形区域ABCD，R1表示正方形区域A1B1C1D1，R2表示正方形区域A2B2C2D2。那么R∩R1表示正方形区域BOD1M，R∩R2表示矩形区域A2FND2，R1∩R2表示矩形区域A2B2GE，R∩R1∩R2表示正方形区域A2FOE个正方形所盖住的部分为R∪R1∪R2。如果用|R|表示区域R的面积，那么根据容斥原理可得 |R∪R1∪R2|=|R|+|R1|+|R2|-|R∩Rl| -|R∩R2|-|R1∩R2|+|R∩R1∩R2| =62+52+22-（32+2×1+1×2）+12 =53 答：三个正方形所盖住的面积为53。 例7 某班学生手中分别拿有红、黄、蓝三种颜色的球。已知手中有红球的共有34人，手中有黄球的共有26人，手中有蓝球的共有18人。其中手中有红、黄、蓝三种球的有6人。而手中只有红、黄两种球的有9人，手中只有黄、蓝两种球的有4人，手中只有红、蓝两球的有3人，那么这个班共有多少人？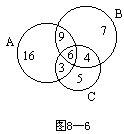（1986年初一迎春杯数学竞赛试题） 分析与解：此题用填写文氏图各区域元素个数的方法来解较为简便，设A、B、C分别表示手中有红球、黄球、蓝球的人的集合。由题意可逐一填出各区域元素的个数（如图）。所以全班共有 16+7+5+9+4+3+6 =50（人） 答：这个班共有50人。 这个题目也可以列式计算如下： （34+26+18）-（9+4+3）-2×6=50（人） 例8 求1到200的自然数中不能被2、3、5中任何一个数整除的数有多少？ 解： 设A=｛1到200中间能被2整除的数｝， B=｛1到200中间能被3整除的数｝， C=｛1到200中间能被5整除的数｝。 那么，A∩B=｛1到200中间能被2×3整除的数｝， A∩C=｛1到200中间能被2×5整除的数｝， B∩C=｛1到200中间能被3×5整除的数｝， A∩B∩C=｛1到200中间能被2×3×5整除的数｝。 设［x］表示小于等于x的最大整数，那么 ｜A｜=［200/2］=100，｜B｜=［200/3］=66， ｜C｜=［200/5］=40，｜A∩B｜=［200/6］=33， ｜A∩C｜=［200/10］=20，｜B∩C｜=［200/15］=13， ｜A∩B∩C｜=［200/30］=6。 根据容斥原理，1到200的自然数中至少能被2，3，5中一个数整除的数共有 |A∪B∪C|=|A|+|B|+|C|-|A∩B| =|A∩C|-|B∩C|+|A∩B∩C| =100+66+40-33-20-13+6=146（个） 所以1到200的自然数中不能被2，3，5中任何一个数整除的数共有 200-146=54（个） 习题八 1.某班有团员23人。这个班里男生共20人，问这个班女生团员比男生非团员多多少人？ 2.纸片面积为7，一张边长为2的正方形纸片，把这两张纸片放在桌面上覆盖的面积为8，问两张纸片重合部分的面积是多少？ 3.从1到100的自然数中， （1）不能被6和10整除的数有多少个？ （2）至少能被2，3，5中一个数整除的数有多少个？ 4.盛夏的一天，有10个同学去冷饮店，向服务员交了一份需要冷饮的统计表：要可乐、雪碧、果汁的各有5人；可乐、雪碧都要的有3人；可乐、果汁都要的有2人；雪碧、果汁都要的有2人；三样都要的只有1人。证明其中一定有1人这三种饮料都没有要。 5.对100个学生课外学科活动的调查结果如下：32人参加数学小组；20人参加英语小组，45人参加生物小组。其中15人既参加了数学小组又参加了生物小组；7人既参加了英语小组又参加了数学小组；10人既参加了英语小组又参加了生物小组。还有30人没有参加上述任何一个学科小组。 （1）求三个学科小组都参加的人数。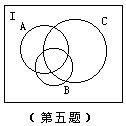 （2）在文氏图的八个区域内填入相应的学生人数。其中A、B、C分别表示参加数学、英语和生物小组的学生的集合。被调查的100个学生的集合为全集I。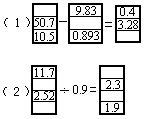 测试题（一） 1.在□里填上适当的数。 2.化简。 3.计算 4.在100名选手间进行乒乓球单打淘汰赛，每场能分胜负。问冠军产生时，共举行了几场比赛。 5.有一座楼高19层，相邻两层之间都有19级台阶，小红从一层走到13层，一共要登多少级台阶？ 6.学校第一次买7个篮球3个足球共花256元，第二次买4个篮球3个足球共花172元，1个篮球、1个足球各多少元？ 7.下面各数中，那个数是分别被3、5、7除后所得余数依次为1、1、5的最小自然数。 （A）166（B）151（C）145（D）以上都不对。 8.若数列a1，a2…，a1993，…中，从第三项开始，每一项为前二项之和，已知a1=12，a2=13，问第1993项（a1993）被3除的余数是多少？ 9.前106个自然数中，既非完全平方数又非完全立方数的数有几个？ 10.左下图是由20个棱长都是1厘米的小正方体拼成的几何体，求它的表面积是多少？ 11.右上图是在一个边长为4厘米的正方体的前后、左右、上下各面的中心位置上，挖去一个底面圆半径为1厘米，高为1.5厘米圆柱体后，得到的一 12.唐僧师徒四人路过一村，发现有人说实话，有人说假话。一天唐僧命孙悟空找来四人，问他们是说实话的还是说假话的人？四人回答如下：“甲说：“我们四人全说假话。”乙说：“我们四人中只有一人说假话。”丙说：“我们四人中有两人说假话。”丁说：“我是说实话的人。”请判断丁是说实话还是说假话？ 13.在桌子上有七张纸片，从中取出若干张，每张都剪成七块，放在桌子上；再从桌子上取出若干张，每张又都剪成七块，都放在桌子上；……问能否在某一时刻，在桌子上出现1990块？1991块？1992块？1993块？

本文地址：http://www.45fan.com/a/question/44692.html